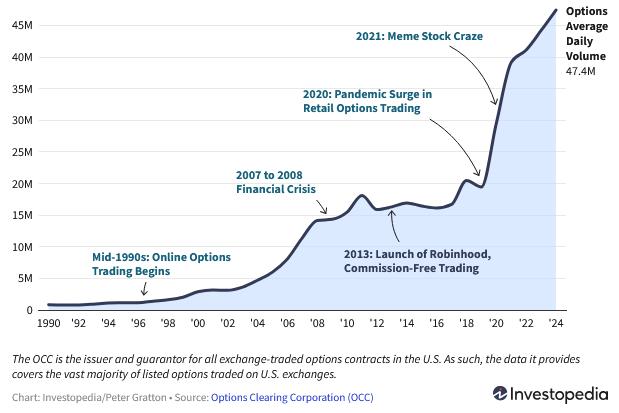
TradingKey - Over the past three decades, the U.S. options market has undergone unprecedented expansion. According to statistics from the Options Clearing Corporation (OCC), retail options trading surged after the 2020 pandemic outbreak, with trading volumes rising rapidly. The 2021 "meme stock frenzy" further propelled volumes to new highs. By 2024, the U.S. options market had reached an average daily trading volume of 47.4 million contracts—nearly exponential growth compared to the early 1990s.
(Source: Investopedia)
Amid this explosive growth in trading activity, investors are increasingly focusing on options trading, where pricing is inseparable from execution. The formation of options prices stems from the interplay of market dynamics, time dimensions, and volatility. Even contracts with similar strike prices and underlying assets often exhibit price differences that reflect the combined state of their intrinsic value and time value.
Options prices are typically calculated using complex mathematical methods, such as the Black-Scholes model and the binomial pricing model. However, this article will focus on the fundamental components of the option premium. By analyzing the interaction between intrinsic value and time value, we clarify the core logic of options pricing. Understanding these elements enables investors to objectively evaluate trading timing and risk-return characteristics, providing a theoretical foundation for practical implementation.
What Is Options Pricing?
The options price, also known as the option premium or rights fee, is the cost paid by the buyer of an options contract to acquire the right to trade the underlying security at a predetermined price at a specific future time. Options pricing mechanisms are complex and influenced by multiple factors, with their core value primarily reflecting the potential profitability of the contract. The buyer pays this fee to secure trading rights, while the seller assumes corresponding obligations in return.
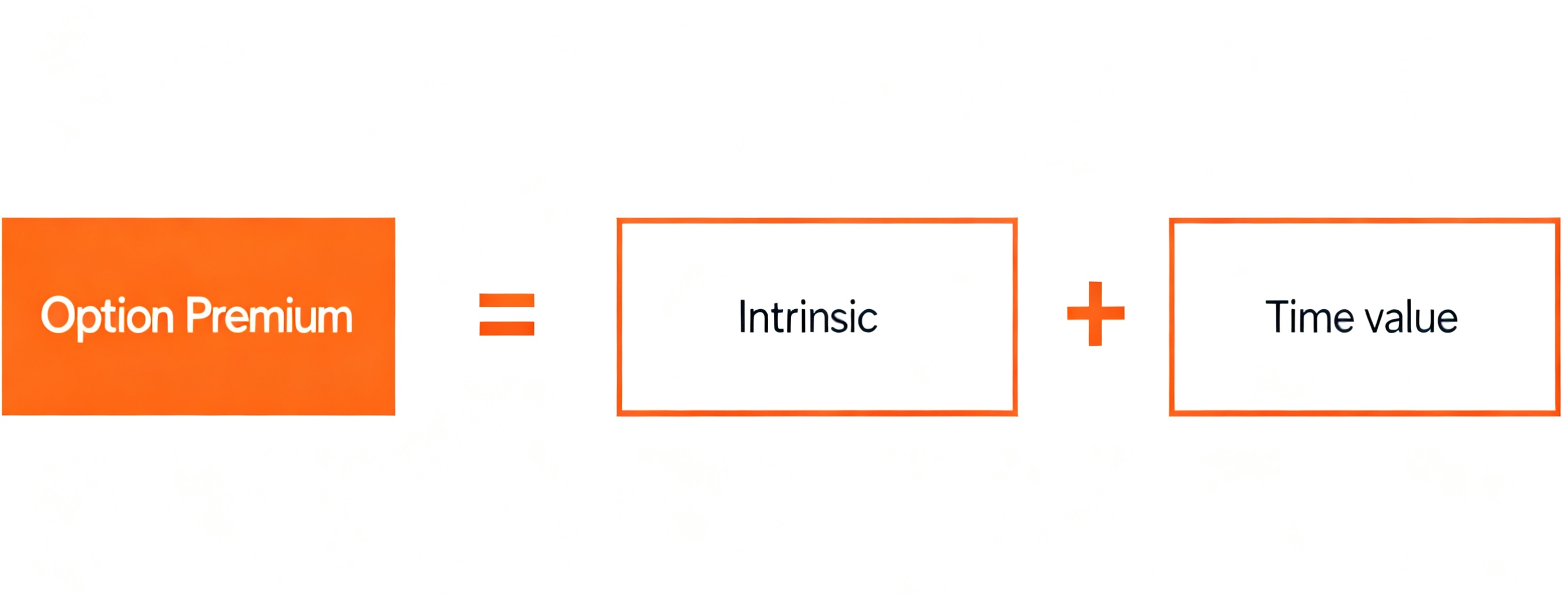
As the central indicator of options trading, the options price directly reflects the contract’s potential profit margin. Its level is closely tied to the option’s moneyness status. This price consists of two components: intrinsic value—the actual difference between the underlying asset’s current price and the strike price—and time value, which represents expectations of additional gains possible within the remaining time until expiration.
Intrinsic Value
The intrinsic value of an option refers to the immediate profit obtainable if the contract is exercised under current market conditions. It is the most intuitive part of the options price, reflecting the difference between the underlying asset’s current price and the strike price.
Intrinsic value is one component of the option’s total value (premium), combining with time value to form the option’s market price. When an option contract expires, its value reduces solely to intrinsic value, as time value diminishes to zero.
It must be clarified that intrinsic value reflects only the immediate exercise value of the option and does not include the premium (option fee) paid by the investor when purchasing the option. Therefore, when evaluating the actual profit from an options trade, the initial premium payment must be factored in.
- Calculating Intrinsic Value for Call Options
The intrinsic value of a call option equals the underlying asset’s current price minus the strike price, with the result capped at zero:
Intrinsic Value (Call Option) = MAX(0, Underlying Asset Price - Strike Price)
For example, if a stock trades at $110 and the call option’s strike price is $100, the intrinsic value is $10 ($110 - $100 = $10). If the stock price is $95 with the same $100 strike price, the intrinsic value is $0 ($95 - $100 = -$5, but negative values are disregarded and set to $0).

- Calculating Intrinsic Value for Put Options
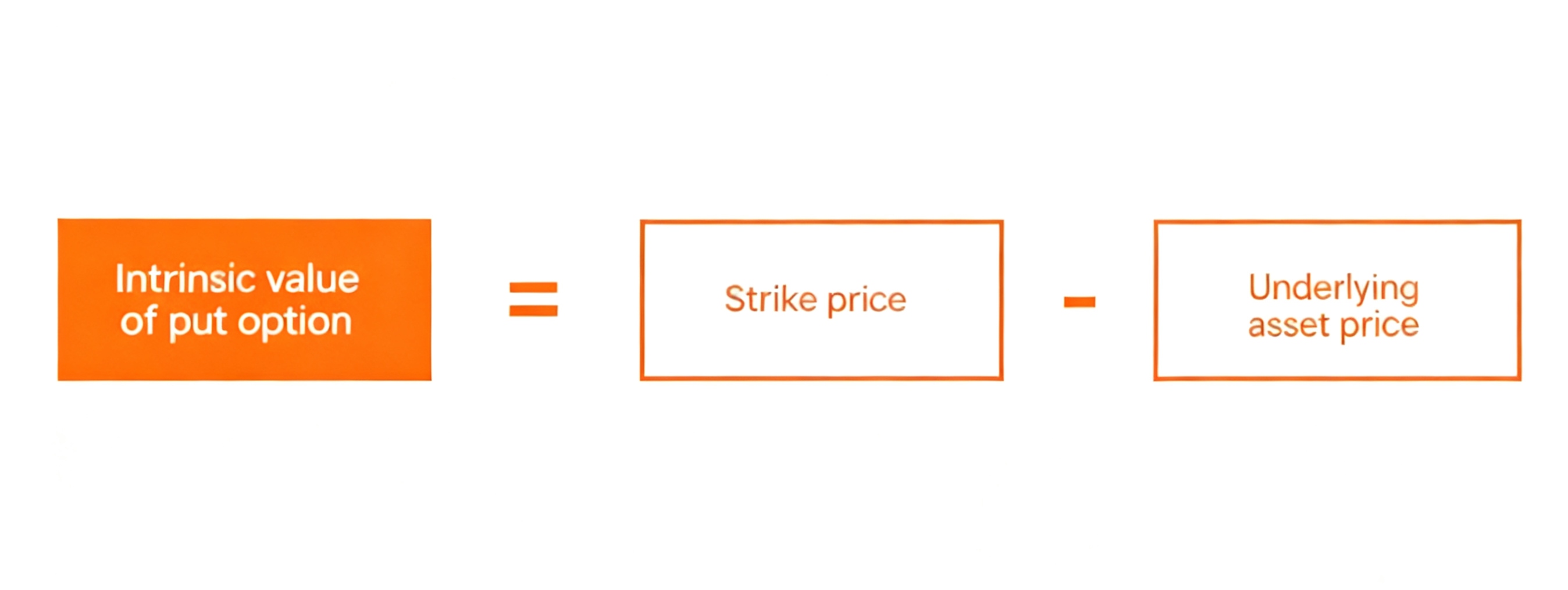
The intrinsic value of a put option equals the strike price minus the underlying asset’s current price, also capped at zero:
Intrinsic Value (Put Option) = MAX(0, Strike Price - Underlying Asset Price)
For example, if a stock trades at $90 and the put option’s strike price is $100, the intrinsic value is $10 ($100 - $90 = $10). If the stock price is $110 with the same $100 strike price, the intrinsic value is $0 ($100 - $110 = -$10, but negative values are disregarded and set to $0).
Time Value
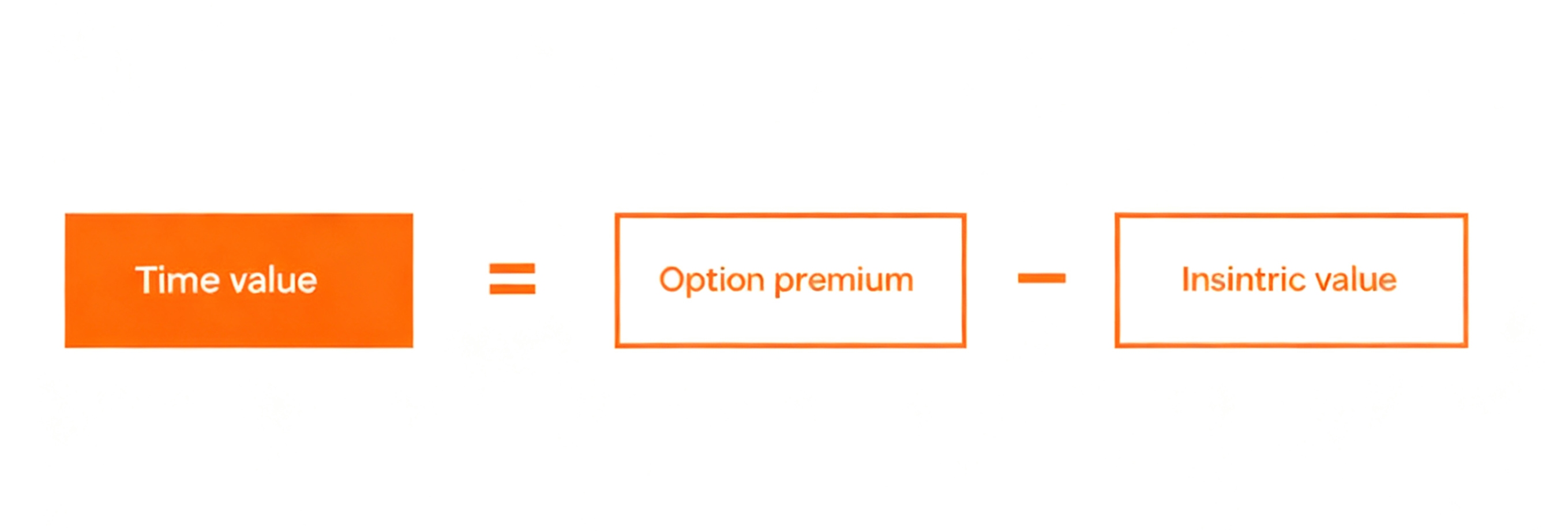
Time value is the portion of an option's price that exceeds its intrinsic value, also known as extrinsic value. It represents the potential value an option may gain before expiration due to possible price movements in the underlying asset. Time value exists because of the finite duration of options contracts—the farther the expiration date, the greater the opportunity for the underlying asset price to move favorably for the option holder, thereby increasing the option’s value.
Longer time periods bring higher profit risks. Conversely, as an options contract approaches expiration, its value declines. This occurs because the security underlying the options contract has less time to be used for profitable maneuvers.
For example:
When a stock trades at $100, a one-month call option with a $90 strike price costs $11.50. Its intrinsic value is $10 ($100 - $90), and its time value is $1.50 ($11.50 - $10).
The same $90 strike call option with a nine-month expiration costs $14.00, giving it a time value of $4.00 ($14.00 - $10).
This difference shows that options with the same intrinsic value but longer durations carry higher time value.
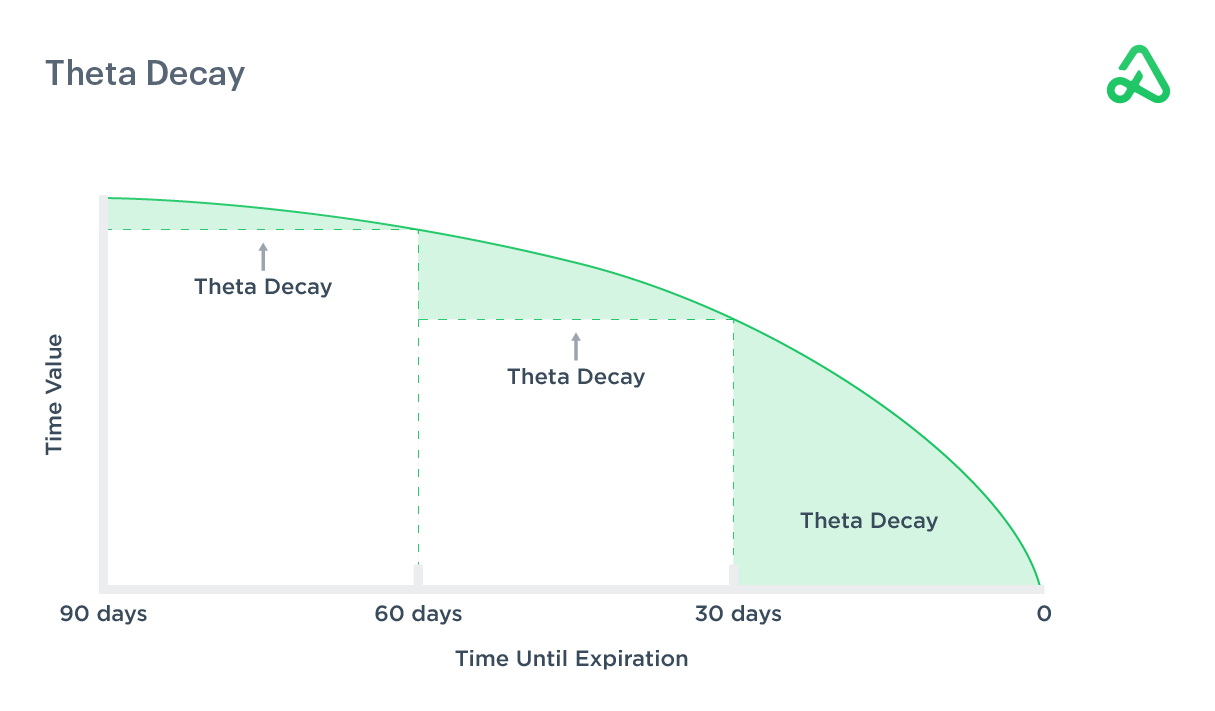
Time Value Decay Characteristics
The decay of an option’s time value exhibits significant non-linear characteristics and is not evenly distributed across the contract’s lifespan.
In the early stages of an option’s life, time value decays relatively slowly—typically losing only one-third of its total time value. However, in the latter half of its lifespan, the decay rate accelerates sharply, with the remaining two-thirds of time value often vanishing rapidly within a short period. Decay peaks dramatically in the final 30 days, a phenomenon critically important to options trading strategies.
The speed of time value decay is measured by the Greek letter Theta (θ), which quantifies the reduction in option value per unit of time.
For instance, a 60-day option typically loses less time value between day 60 and day 30 than between day 30 and expiration—visually demonstrating accelerated decay. This non-linearity stems from the narrowing time window: as expiration nears, opportunities for favorable price movements in the underlying asset diminish, causing the market to price time value downward.
In options trading, time value decay presents both challenges and opportunities. For buyers, this process represents continuous value erosion, particularly pronounced near expiration. For sellers, it creates opportunities to profit from accelerating time decay.
It is noteworthy that while time value systematically declines as expiration approaches, other Greek parameters like Gamma and Vega may intensify during this phase, partially offsetting or altering Theta’s decay effect.
(Source: Option Alpha)
Options Moneyness Overview
- In-the-Money (ITM) Options
Call Option: Underlying asset price > Strike price
Put Option: Underlying asset price < Strike price
Characteristic: ITM contracts possess positive intrinsic value and also include time value.
- At-the-Money (ATM) Options
Call/Put Option: Underlying asset price = Strike price
Characteristic: ATM contracts have the maximum extrinsic value or time value, with intrinsic value close to zero.
- Out-of-the-Money (OTM) Options
Call Option: Underlying asset price < Strike price
Put Option: Underlying asset price > Strike price
Characteristic: OTM contracts have no intrinsic value because, based on the current price of the underlying security and the contract’s strike price, these contracts are in an "out-of-the-money" state. For OTM call options, the underlying security’s price is below the option’s strike price.
The table below presents this information clearly:
Call Option | Put Option | |
In-the-money (ITM) | Stock price > Strike price | Stock price < Strike price |
At-the-money (ATM) | Stock price = Strike price | Stock price = Strike price |
Out-of-the-money (OTM) | Stock price < Strike price | Stock price > Strike price |
- Deep In-the-Money Options (DITM)
Deep in-the-money options refer to contracts where the strike price significantly diverges from the underlying asset’s current price.
Specifically, for call options, the strike price must be substantially lower than the underlying asset’s market price; for put options, the strike price must be substantially higher than the underlying asset’s market price.
Typically, in-the-money option contracts with a value exceeding $10 are considered deep in-the-money. The value of such options heavily depends on intrinsic value, with other pricing factors like time value and volatility having minimal impact. Near expiration, the price of deep in-the-money options is almost entirely determined by intrinsic value, and the time decay effect is relatively limited.
- Deep Out-of-the-Money Options (DOTM)
Deep out-of-the-money options exhibit a severe misalignment between the strike price and the underlying asset’s current price. For call options, the strike price is significantly higher than the market price; for put options, the strike price is significantly lower than the market price.
Since these contracts possess no intrinsic value, their entire worth stems from external factors such as time value, implied volatility, and market expectations. For a deep out-of-the-money option to hold value at expiration, the underlying asset price must undergo substantial movement to surpass the strike price threshold. Consequently, its value is highly sensitive to the magnitude of price fluctuations in the underlying asset. Time decay exerts a pronounced impact on pricing, particularly near expiration, where value may rapidly approach zero.Stock price > Strike price
What Factors Determine Options Pricing?
- Underlying Asset Price
As the most critical variable in options pricing, fluctuations in the underlying asset price directly affect the value of options contracts.
When the underlying asset price moves in a direction favorable to the option holder, the option’s intrinsic value increases accordingly.
Take a call option as an example: if a stock’s current market price is $150, and you hold a call option with a $145 strike price, the option already has $5 of intrinsic value. As the stock price rises to $160, this intrinsic value expands to $15, and the option’s overall value increases correspondingly.
- Strike Price
The strike price is a pre-set price at which the option holder can buy (call option) or sell (put option) the underlying asset.
This predetermined transaction price determines whether the option has immediate profit potential. The closer the underlying asset’s market price is to the strike price, the more pronounced the time value premium becomes—especially in the "in-the-money" (ITM) state.
Assume a stock’s current market price is $150:
Holding a call option with a $140 strike price yields an immediate $10 profit upon exercise ($150 - $140), placing it deep in-the-money.
A call option with a $170 strike price is out-of-the-money (OTM), as $150 < $170, and exercising it would result in immediate loss.
- Volatility
Volatility is the lifeblood of the options market, defining the vitality and uncertainty of price movements. If the underlying asset price remains stagnant like still water, options would lose their time value, becoming simple contracts with only intrinsic value. It is precisely this price fluctuation that grants options their unique investment appeal.
Volatility comes in two forms: implied volatility (the market’s forecast of future volatility) and historical volatility (past volatility).
When volatility in the underlying asset price intensifies, the values of both call and put options rise simultaneously. Greater price swings increase the probability of the underlying asset surpassing the strike price, thereby enhancing the option’s profit potential.
- Time to Expiration
Reducing time to expiration decreases the time value of a call option, leaving only its intrinsic value at expiration. The longer the remaining term, the greater the potential for the underlying asset price to move favorably, and the richer the option’s time value becomes. This time premium constitutes a significant component of the option’s price.
- Dividends
Dividends exert significant yet often underestimated influence on options pricing. When the underlying stock is expected to pay dividends, the market preemptively reflects this information, affecting the option’s pricing structure.
Since stock prices typically drop after the ex-dividend date by an amount close to the dividend payment, this expectation is reflected in option prices. Specifically, high expected dividends reduce call option premiums while increasing put option premiums.
- Interest Rates
Rising interest rates cause call option premiums to increase and put option premiums to decrease. Any change in interest rates impacts options valuation, thereby influencing the underlying asset price, strike price, market volatility, and dividend payments.
In a high-interest-rate environment, the reduced opportunity cost of holding cash makes options trading more attractive. For instance, after the Federal Reserve announces a rate hike, call options on bank stocks may rise in value because high rates typically benefit bank profitability.
From a capital efficiency perspective, buying call options offers advantages over directly purchasing stocks—investors can control the same quantity of assets with less capital, while the remaining funds can generate higher returns in a high-rate environment. Simultaneously, rising rates increase the cost of borrowing to buy stocks, making options a more economical choice. Although interest rate changes typically have less impact on options prices than volatility and underlying asset price movements, they remain an indispensable factor in pricing models.
Application of Options Pricing Strategies
Mastery of options pricing principles provides investors with diverse trading strategy options, enabling them to flexibly adjust portfolios based on market expectations and risk preferences. A deep understanding of options price formation mechanisms helps investors make more precise decisions across varying market environments.
- Risk Hedging Strategy
Knowledge of options pricing empowers investors to construct effective risk hedging mechanisms. When holding an underlying asset and concerned about downside risk, purchasing put options provides downside protection, limiting potential losses to the premium paid.
This strategy functions like insurance: while there is a risk of the option expiring worthless (resulting in premium loss), it effectively mitigates systemic risks from sharp declines in the underlying asset. The value of hedging lies in its certainty—regardless of market volatility, the investor’s maximum loss is predetermined and locked in advance.
- Price Speculation Strategy
For investors with higher risk tolerance, options pricing knowledge offers more efficient risk management tools. By analyzing expected changes in volatility, interest rates, and time decay, traders can design targeted speculative strategies.
- Income Enhancement Strategy
Selling options is an effective method to generate stable cash flow, particularly suitable for volatile market conditions. Traders often choose to sell out-of-the-money options to capitalize on accelerated time decay and collect premium income.
For example, selling call options while holding the underlying stock (covered call strategy) generates premium income while allowing the stock to be sold at a predetermined price if it rises to the strike price.
However, such strategies carry potentially unlimited risk, especially during periods of extreme market volatility. Therefore, when employing income enhancement strategies, investors must rigorously assess risk tolerance and implement stop-loss mechanisms or complementary hedging tools to control potential losses.


